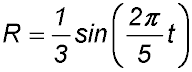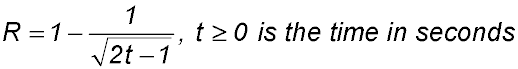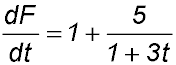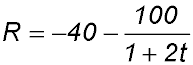Calc - applics - RofC

The questions on this page focus on:

given a quantity;
given a rate of change.

Given the quantity.	1. As NBN cable is unwound from a cylinder, the mass of cable remaining on the cylinder decreases. The mass (M kg) of wire remaining on the cylinder after t minutes can be calculated by the formula . (i) Find the initial mass of the wire on the cylinder. (ii) Find the time taken to remove all the wire from the cylinder. (iii) Find the rate at which the wire is being removed from the cylinder when half the wire has been removed. Answer.(i) Initial mass = 200 kg. (ii)Time = 35 mins. (iii) Rate = -40/7 (or -5.71) kg/min at 11.25 secs.
	2. Some yabbies are introduced into a small dam. The number in the population can be modelled with the equation where t is the time in months after the yabbies were introduced into the dam. (i) Show that the rate of growth of the size of the population can be described by (ii) Find the range of the function y, justifying your answer. (iii) Show the rate of growth in the size of the population can be rewritten as . (iv) Hence find the size of the population when it is growing at its fastest rate. Answer.(ii) 10 ≤ y < 200. (iv) Max rate at y = 100.
	3. An Olympic sized swimming pool is being emptied. The volume of water in the pool in litres after t hours is given by the equation L = 312 (20 - t)³ (i) What is the approximate volume of water in an Olympic sized swimming pool? (ii) How long does it take the pool to empty? (iii) Find the rate at which the pool is emptying after 10 hours. (iv) When is the pool emptying at a maximum rate? Answer.(i) Approx. 2.5 million litres. (ii) Empty after 20 hours. (iii) Emptying at 93,600 L/hr. (iv) Maximum rate of emptying is at 20 hours.
	4. During a certain influenza epidemic, the proportion of the population in a school who are infected is given by where t is the time in weeks since the start of the epidemic. (i) What proportion of the school's population was infected after 3 weeks? (ii) Find when the epidemic peaks and at what is the maximum infection rate? Answer.(i) 23.1%. (ii) Peaks at 25% after 2 weeks.
	5. The volume V cm³ of a balloon is increasing such that its volume at any time t seconds is given by Find the exact rate at which the volume is increasing at t = 2 seconds. Answer.Rate = (10π)/3 cm³/sec.
	6. A water tank which is initially full is being emptied. The remaining quantity of water Q litres in the tank at any time t minutes after the tank starts to empty is given by Q = 1000 (20 - t)² where 0 ≤ t ≤ 20. (i) How much water was in the tank initially? (ii) Show that . (iii) At what time is the water flowing out at the rate of 20,000 litres per minute? (iv) At what rate is the tank emptying when the tank is half full? Answer.(i) Q = 400,000 lit. (iii) 10 minutes. (iv) Emptying at -20,000√2 lit/min.
	7.
	8.
	9.
Given the rate	10. A colony of bacteria is being studied. After t seconds, the rate at which the population is changing is given by 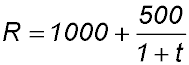where R measures the change in the number of bacteria per second. (i) What is the rate of change in the number of bacteria in the colony at the beginning of the experiment? (ii) Sketch the graph of R against t. (iii) In the first 9 seconds, what will be the total increase in the number of bacteria (answer to nearest hundred). Answer.(i) Rate of change when t = 0 is 1500 bac/sec. (iii) 10,200 bacteria in 1st 9 secs.
	11. A tank filled with water is accidentally punctured when an accident punctures a hole in its side. As water began to pour out, the volume of water in the tank changed at a rate of R = t² - 9t - 10 litres/minute for 0 ≤ t ≤ T where t is the time in minutes after the accident and the water began to flow out. Initially the tank held 400 litres of water. (i) What is the largest value of T for which the expression for the rate (R) is physically reasonable? Explain your answer. (ii) Calculate the exact amount of water left in the tank once the water stops leaking. Answer.(i) Longest time is 10 mins. (ii) Volume = 183.33 litres.
	12. Oil from a cargo ship began to leak while the ship was docked in a harbour. Several hours later, authorities began the clean-up operation. The rate at which the oil was removed is described by the equation 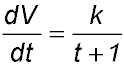where k is a constant, t is the time in hours after the start of the clean-up operation and V is the volume of oil removed in kilolitres. By 10.00 am, x kilolitres of oil were removed. Two hours later, an additional 4 kilolitres had been removed and after three more hours, another 4 kilolitres had been removed. (i) Find an expression for the volume of oil removed in terms of k and t. (ii) At what time did the clean-up operation start? Answer.(i) V = klog_e (t + 1) + c. (ii) Clean-up began at 7 am.
	13. A spherical balloon has a radius of 20 cm. It is then inflated at a constant rate of 100 cm³ per second. (i) Show that the volume of the balloon at any time t can be expressed as V = 100t + 33,510. (ii) How long, to the nearest second, will it take for the volume of the balloon to reach 100 litres (1000 cm³ = 1 litre). Answer.(ii) 665 secs = 11.08 mins.
	14. An adult's breathing cycle is 5 seconds long. For time t seconds, 0 ≤ t ≤ 2.5, air is taken into the lungs. For 2.5 < t ≤ 5, air is expelled from the lungs. The rate R litres/second at which air is taken in or expelled from the lungs can be modelled approximately by the equation Using this model, how many millilitres of air does an adult take into their lungs during one breathing cycle? Answer.about 530 mls of air.
	15. A tank is emptied by a tap from which the water flows so that, until the flow ceases, the rate of flow after t minutes is R lites/minute where R = -(t - 6)². (i) What is the initial rate of flow? (ii) How long does it take to empty the tank? (iii) How long will it take (to the nearest second) for the flow to drop to 20 litres/minute? (iv) How much water was in the tank initially? Answer.(i) 36 litres/min. (ii) 6 minutes. (iii) 1.53 mins. (iv) 72 mins.
	16.
	17. A rainwater tank is initially empty. The rate R litres/sec at which water is entering the tank is given by (i) Show that, after one minute, the tank is filling at an approximate rate of 0.91 litres/sec. (ii) The tank is full to its capacity after 66 minutes, Explain why the capacity of the tank is less than 3,960 litres. (iii) Determine the capacity of the tank. Answer.(ii) as R < 1, capacity < 66*60 = 3,960 litres. (iii) max capacity = 3,871 litres.
	18. The rate at which fuel is being pumped from a full tank is given by where F kilolitres is the amount of fuel pumped out in the first t minutes. (i) Find the rate at which the fuel is being pumped out in the first 8 minutes. (ii) Draw a sketch of as a function of time. (iii) Find the amount of fuel pumped out after 8 minutes (to the nearest litre). Answer.(i) Rate = 1.2 lit/min. (iii) Amount of fuel = 13 litres.
	19. The rate R, in micrograms per minute, at which the amount of snake venom is neutralised t minutes after the injection of an anti-venom is given by (i) What is the initial rate of neutralisation when the anti-venom is injected? (ii) What is the rate of neutralisation 2 minutes after the administration? (iii) Show that the rate at which the snake venom is neutralised will never rise above -40 micrograms/minute. Interpret what that value implies. (iv) Draw a sketch of R as a function of t. (v) Calculate the amount of the venom neutralised in the first hour after the anti-venom is injected. (vi) Snakes inject varying degrees of venom depending on their type and maturity. If a snake injected a fairly typical amount of venom - say 140 mg - use your answer to part (v) and your graph to estimate how long it would take for the vaccine to neutralise approximately that amount of venom. Answer.(i) Initial rate = -140 μgm/min. (ii) At 2 mins, R = -60 μgm/min. (v) Amount in 1 hour = 2,640 μgms. (vi) About 58 hours.
	20. A circular metal plate of area A cm² is being heated. As it heats, the radius increases at a constant rate of 0.15 cm/h. (i) Express the expansion rate as a derivative function. (ii) Write a complete integral statement with which to calculate the radium after t hours of heating given that initially the plate had a radius of 6 cm. (iii) Determine the exact area of the plate after 8 hours. Answer.(i) dr/dt = 0.15. (ii) r = 0.15t + 6. (iii) A = 49π u^2>.
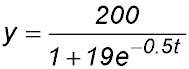
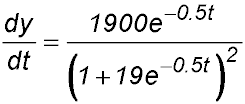
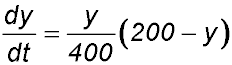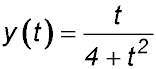
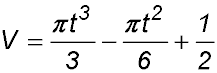
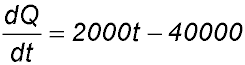